Archive for June, 2017

Keeping parolees out of jail
Dr. Brett Garland, head of the department of criminology and criminal justice at Missouri State University, has been studying the criminal justice system for over a dozen years. He’s published more than 40 journal articles, book chapters and other scholarly works, mostly on topics pertaining to correctional issues.
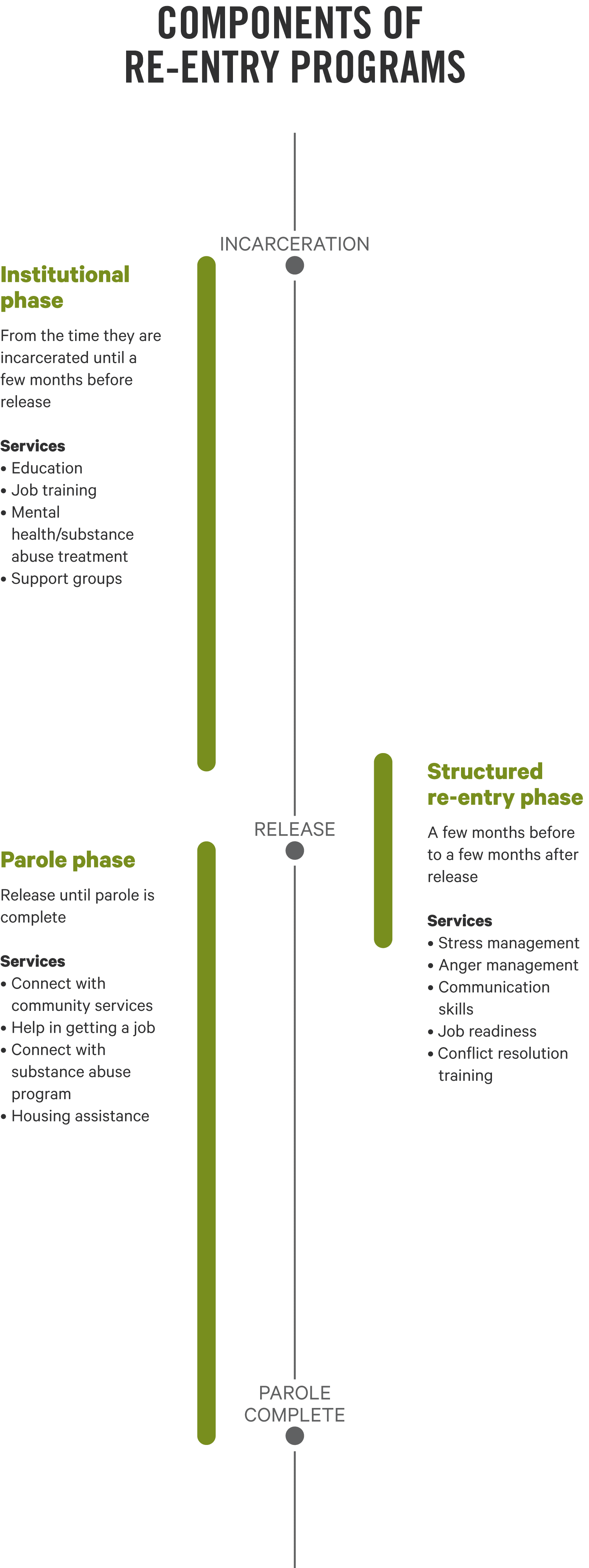
One primary area of research for Garland is prisoner re-entry. That’s the phase from a few months before a prisoner is released to a few months after release.
“That’s the time period where offenders are really starting to transition mentally; they’re getting themselves ready for the release,” he said.
Which is better? The carrot or the stick?
A study Garland did with co-authors Dr. Eric Wodahl and Dr. Scott Culhane from the University of Wyoming and Dr. William McCarty from the University of Illinois at Chicago found that offenders are most successful in following the terms of their parole when a combination of sanctions and rewards are used.
“We know from psychology and from behavioral learning theory that rewarding people for things they do right is even more important than punishing people for something they do wrong. Our study confirmed that this principle holds true for criminal offenders,” said Garland. “In the last decade or so, there’s been renewed attention to incorporating incentives and using a true behavioral model when monitoring people who are on probation and parole.”
Garland has collaborated with Wodahl on a number of projects. Wodahl is a former probation and parole officer and said he thinks this research can help supervision officers do their jobs more effectively.
“I believe this research has the capacity to help lessen our reliance on prison in this country,” he said. “A large portion of prison inmates are incarcerated for violating the conditions of their probation or parole supervision. The use of sanctions and incentives has been shown to lead to fewer revocations and fewer people being sentenced to prison.”
Garland said to gain maximum compliance from a probationer or a parolee, officers must be committed to utilizing reinforcements whenever suitable opportunities arise.
Time off is best incentive
Another study by Garland and Wodahl, in Colorado, examined the value that offenders ascribe to various types of incentives relevant to probation.
The researchers interviewed 200 offenders and presented 16 options, including monetary incentives, reductions in supervision time and travel opportunities, among others.
“The perceived effect from the offender’s standpoint was that getting time off of a sentence was more important to them and therefore more valuable than all other options,” said Garland. “The policy implication here is that you don’t necessarily have to spend a lot of money to provide good incentives for offenders.”
As the cost to incarcerate a person continues to increase, finding ways to keep people out of prison may be the best solution. Garland hopes his work will help do just that.
- Story by Andrea Mostyn
- Photo by Kevin White
Further reading

Prove it: Math makes the world go ‘round
Enter mathematics
Mathematically, such laws are expressed through differential equations or, more generally, dynamical systems.
Dr. Shouchuan Hu, professor of mathematics at Missouri State University, has devoted his career to the study of differential equations, dynamical systems and nonlinear analysis. This area of mathematics largely asks theoretical questions. More often than not, it is impossible to write down the explicit solution of the differential equations that describe physical processes.
“Often in mathematics we’ve been taught to say that graphics will show you or give you some intuition and ideas, but they will never serve as a proof.” — Dr. Shouchuan Hu
Therefore, Hu and others in this field investigate whether or not solutions exist. If a solution exists, the mathematician determines if the solution is unique and under what conditions and studies the qualitative behavior of the solution — a topic that often relates back to behavior of physical systems.
As an example, think about planetary motion.
“Certainly if you look at the planet orbits, they are periodic,” said Hu. “Such motions can be governed by a common differential equation, and sometimes a solution of such an equation is exactly the orbit of this motion.”
The ideas and methods used to study the differential equations of planetary motion can be applied to biological questions, like whether an animal species population could be periodic or environmental conditions such as seasonal weather changes.
Collaborative nature of math
One of Hu’s long-term collaborators is Dr. Nikolaos Papageorgiou, professor of mathematics at National Technical University in Athens, Greece. Together they produced two textbook volumes on multivalued analysis – a subfield of nonlinear analysis – that has been praised for its exhaustive depth in the field.
Papageorgiou is excited by the number of non-mathematicians who benefit from their work.
“Almost all interesting problems in nature and society are highly nonlinear and the traditional tools of classical linear functional analysis do not suffice to tackle them,” said Papageorgiou. “Today, many nonmathematical disciplines use the notions, techniques and theories of nonlinear analysis to come up with more realistic models of the phenomena they study and to analyze them.”
Mathematically on the map
When Hu came to Missouri State in 1987, he was the first professor from mainland China to join the faculty, and he quickly made a name for himself in his field. In 1995, he helped launch the international journal Discrete and Continuous Dynamical Systems and has served as the editor-in-chief ever since. He also serves as the co-editor-in-chief for the international journal Communications on Pure and Applied Analysis.
Though it can be a time-consuming and intimidating task to produce a peer-reviewed academic journal, he is proud of the quality of contributors it attracts. Seven Fields Medal recipients have contributed papers over the years.
“The Fields Medal – it’s basically like a Nobel Prize for mathematicians. In a way it’s even more prestigious than the Nobel Prize because it’s only distributed every four years,” he said.
Photo by Bob Linder
He’s also been able to bring that level of esteem to one of his other notable achievements: In 1996, Hu was the principal organizer of an international conference on Dynamical Systems, Differential Equations and Applications and has served as the chairman for this conference since its inception.
Many Field medalists have presented their research at this biennial conference, which has grown to be the largest conference in the field. From 250 attendees in the first year, it catapulted to regularly include 1,500-2,500 attendees. This international group had its first meeting at Missouri State, and Hu said, it put the university mathematically on the map.
“It’s the largest, most attended conference in the field,” Hu said. “This conference series has become so influential, and it has fulfilled a need in the scientific and mathematic community. Everywhere you go, at least in every mathematical department, some of the faculty will know us.”
In 2000, Hu helped form, and currently directs, the American Institute in the Mathematical Sciences. AIMS is now responsible for the organization of the conference, and it publishes 14 journals in a variety of areas of the mathematical sciences, and publishes a book series related to dynamical systems and applications. To a large extent, AIMS represents Hu’s vision toward furthering mathematical research.
He has also published 76 refereed research articles – many in collaboration with Papageorgiou – in the area of differential equations and dynamical systems since becoming a faculty member at Missouri State.
- Story by Nicki Donnelson
- Photos by Bob Linder